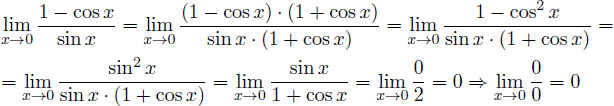Деление на ноль
Материал из Lurkmore
 | Эта статья рассказывает о какой-то антинаучной хуйне. Если вы — физик, химик, биолог или просто слишком хорошо помните школьную программу соответствующего курса, вам лучше ее не читать. В противном случае вы рискуете умереть от смеха. Мы предупредили. |
| « |
Hmmm... no, no... that's wrong... that's not right, either... a divide by zero error here... hmmm... you don't seem to have the intelligence necessary to grasp higher mathematics. | » |
| — Проконсул Грегори из Fallout 2, проверяя результаты испытания ГГ | ||
Деление на ноль (Дивайд бай зиро) — математическое действие, невозможное в элементарной алгебре из-за возникающей при этом неопределённости.
Содержание |
[править] Деление на ноль как мем
Физически (или физиологически) пребывать в процессе деления на ноль вполне можно. Стой себе и дели. То есть, с точки зрения очевидности, делить на ноль можно, никто законодательно же не запрещал. Проблема обычно заключается в том чтобы получить из этого процесса хоть какой-то обоснованный наукой результат (или создать потом заново вселенную).
Деление на ноль давно стало одним из классических образцов математического юмора, поскольку в среде математиков считается, что попытка представить получающуюся в итоге актуальную бесконечность (неотъемлемая часть успешного деления на ноль, в противоположность потенциальной бесконечности из теории пределов) ведёт к сумасшествию совершившего это. Алсо, в обществе прикладных математиков пожелание «делись оно всё на ноль» является аналогом широкоизвестного рецепта «а пошло оно всё в…». Поскольку численность математик-кунов в среде компьютерщиков и истинных хакеров составляет лишь чуть менее чем 42%, этот мем проник и туда, а с возникновением форчана обогатился представлением о том, что удачное деление на ноль неотвратимо вызывает не только безумие самого экспериментатора, но и создание сингулярной аномалии бесконечной массы в точке пространства, где было произведено удачное деление. Со всеми вытекающими последствиями.
Среди менее продвинутых товарищей деление на ноль упоминается в том же смысле, что и умножение на него же. Хуже того, в очень многих статьях этого сайта можно найти это словосочетание именно в ошибочном смысле, противоположном истинному. Это ещё один аргумент в пользу ввода матан-капчи. Или против неё.
[править] Деление на ноль в математике
 | ACHTUNG! Опасно для моска! Министерство здравоохранения Луркмора предупреждает: вдумчивое чтение нижеследующего текста способно нанести непоправимый ущерб рассудку. Вас предупреждали. |
Поле действительных чисел, помимо всего прочего, является аддитивной группой, и ноль — нейтральный элемент этой группы. Множество ненулевых действительных чисел, снабжённое операцией умножения, является мультипликативной группой. Поэтому запиливая ноль в эту группу, мы превращаем её во что-то группой не являющееся, ибо понадобилось бы как минимум запилить туда обратный нулю элемент, который, очевидно, не может быть действительным числом, а если запилить НЕХ как обратку, то ещё больше проблем будет, так как остальные элементы действительные, и понадобилось бы прописать, как они взаимодействуют с обраткой, и даже если всё цивильно получится, то полученное множество уже не будет даже изоморфно привычному множеству действительных чисел. Такие дела.
Поэтому поле действительных чисел называют нетривиальным.
[править] Алгебра
А настоящие быдломатематики знают, что если определить операцию деления на ноль, то тогда выходит, что все числа совпадают, так что лучше на ноль не делить вовсе…
Действительно, пусть у нас есть два произвольных разных числа, a и b, и мы умеем делить на ноль:
0 * a = 0
0 * b = 0
0 * a = 0 * b
делим на 0, и получается
a = b
Таким образом «доказывается», что 2+2=n. (где n=любое число)
0 = 0
(2+2)*0 = n*0
делим на 0, и получается
2+2 = n
Делить на бесконечно малую функцию можно, при этом получается бесконечно большая функция, так что всё довольно тривиально. А вот отношение бесконечно малых (0/0) в народе называют неопределённостью. Для двух данных функций эту неопределённость иногда даже можно раскрыть, пользуясь правилом Лопиталя (взятие производной от числителя и знаменателя, причем, иногда неоднократно). Для подробностей курите соответствующую литературу. Но, всё это, как известно, рассматривается под знаком предела и не имеет никакого отношения к делению на ноль. Бесконечно малая величина? Не ноль, а где-то рядом.
[править] Дельта Дирака
А вот физики и математики знают, что есть такая дельта-функция Дирака, которая равна нулю всюду, кроме 
, а при она равна 1/0. Докажем это. По определению, интеграл дельта-функции равен 1. С другой стороны, интеграл функции, которая равна y на отрезке длины a и равна 0 за пределами этого отрезка, очевидно, равен ay. В нашем случае a=0. Получаем 0y=1. Решая это несложное уравнение относительно y, получаем y=1/0.
На самом деле дельта-функция Дирака — это не функция в обычном понимании, а линейный непрерывный функционал над пространством финитных бесконечно дифференцируемых функций, то есть 
, но это мало кого волнует.
К слову в этой вашей ЕВЕ, один из ангелов (монстров, боромых героями) представлял собой т. н. «море Дирака» — плоскость, содержащую в себе не то пространство, не то его отсутствие… В любом случае, любые объекты физического мира, что тонули в нём, больше не всплывали, что было эквивалентно делению их на ноль.
[править] Деление на ноль и пределы
;
Таким же образом приводятся выражения типа 
/ .
Правило Лопиталя.
Правило гласит, что если функции f(x) и g(x) обладают следующим набором условий:
-
или 
;
-
;
-
в проколотой окрестности a;
- g(x) и f(x) — дифференцируемы в проколотой окрестности a,
тогда существует 
.
Алсо стоит вспомнить про Первый Православный Замечательный Предел, в котором сабж внезапно выдает результат равный 1. Случай подробно описан в Педивикии.
Из соображений политкорректности сабж предпочтительнее называть бесконечно малой величиной, то есть чуть более чем ничем. Но даже несмотря на это адепты матана, стараются всячески избежать деления на бесконечно малую величину (равно как и умножения на бесконечно большую), а потому сабж является идеальным объектом для оттачивания mad skillz у матанфагов.
[править] Нестандартный анализ
Для тех, кому на ноль делить все-таки очень уж хочется, в нестандартном анализе придумали гипердействительные числа; так, например, существует число не равное нулю, но меньшее всех остальных по модулю. Школьные знания здесь не помогут.
[править] Точка зрения прикладной алгебры
Деление — это не атомарная операция, а макрос — взятие обратного по умножению от делителя и умножение на делимое. Например, обратный двойке по умножению — это 0.5, 3/2 — 1.5 и т. д. Операция взятия обратного по умножению определена для всех чисел, кроме нуля (говорят — нуля по сложению). Деление на ноль на самом деле не запрещено, эта операция просто не определена, как перемножение паровоза на ковер. Так-то.
[править] Матан, он такой матан…
Проблема деления на ноль это ещё полбеды. В некоторых областях алгебры делить нельзя вообще. Например, в случаях более абстрактных чисел вообще нельзя ввести деление как таковое (например, седенионов, или других ещё более страшных слов). Связано это с появлением делителей нуля, то есть пар ненулевых элементов, произведение которых равно нулю. А это приводит к появлению вполне осмысленных результатов при делении на ноль. Или-же просто с невозможностью нахождения обратного элемента.
[править] Теоретически поделить на ноль не сложно
процентная доля от числа это число делённое на общее кол-во, но мы то знаем что 0 от нуля составляет 100% а 0 от любого другого числа ∞% следовательно
0/0=1 (-∞;0)⋃(0;+∞)/0=∞/100
[править] Мнение Wolfram|Alpha
Если ввести в Вольфрам 1/0, то получим ~∞, а если 0/0 — INDETERMINATE.
На запрос x=(0/0=1)*1 он отвечает… x=0 (он воспринимает сабж как логическое выражение по типу языка С и таки да: 0/0 не равно единице что он и возвращает нулем…булевым)
[править] Деление на ноль в программировании
В программировании числа целого типа (попытаться) поделить на ноль в принципе можно, но получается какая-то хуита: процессор x86 при попытке выполнить операцию целочисленного деления на ноль формирует особый случай (исключение) с номером 0, вектор которого также находится по адресу 0. Другими словами, процессор славное действие деления на ноль до конца не доводит, а перескакивает в другое место, обычно сообщая юзеру о внезапном просирании всех полимеров. На самом деле, поскольку деление целых чисел осуществляется на микропрограммном уровне как вычитание со сдвигом и при этом признаком окончания процесса является обнуление остатка от делимого, нулевой делитель означает бесконечное число циклов с одинаковым ненулевым результатом. Ч.т.д. А вот и нет. Делимое списывается в остаток и возвращается нуль. Так то!
Зато числа с плавающей запятой делить на ноль можно невозбранно. При афинном представлении бесконечностей получается плюс бесконечность (+INF) или минус бесконечность (-INF) — зависит от знака делимого числа. При проективном представлении — беззнаковая бесконечность (INF) в любом случае. Самое интересное происходит при делении на ноль самого ноля: результатом будет число «Не Число» (NaN, Not a Number).
Альзо, в одной книжке по процессорам Intel сказано, что NaN и Inf — вполне обычные числа. Если не обращать внимания на исключения, то с ними можно производить операции: NaN + <число> = NaN, NaN * <число> = NaN и т. д. и т. п.
В КофеСкрипте при делении числа на ноль возвращается «Infinity».
Алсо, в лаконичном языке программирования J $subj даёт бесконечность, обозначаямую как «_». Адепты данного языка ехидно заявляют, что ошибка при делении на ноль возникает исключительно в головах быдлокодеров, пытающихся освоить мозголомный синтаксис J.
[править] Деление на ноль в образной логике
Если попытаться с помощью образной логики изобразить такой математический процесс как деление, то получится раздача неких предметов неким субъектам. Например: 10 делим на 2 = мать раздаёт 10 яблок двум своим детям поровну, и у каждого в руках оказывается по 5 штук. Поэтому с точки зрения образной логики «деление на ноль» это «отсутствие деления». Скажем, 10 : 0 это 10 яблок, которые никто никому не раздаёт. Деление же ноля на ноль это «пустая корзина, в ней нет ни одного яблока, вот потому их никто никому не раздаёт».
Только это всё чушь, вот тут действительно образная алгебра http://rutube.ru/tracks/4758962.html?v=9dcbc9d87ae73246a5afe722819cc864
[править] Тривия
- В рассказе Леонида Каганова «Гамлет на дне» главный герой под воздействием сектантов ушёл в подземелье и делил на ноль долгое время, пока не появился чудо-спасатель.
- ВИА «Кровосток» в тексте, простите, песни «Сдохнуть» как бы предупреждает: «можно сдохнуть пытаясь делить разные числа на ноль».
- У группы gastel?o есть песня «:0». Текст песни подтверждает [1], что его придумавший явно изящно поделил…
- Деление на ноль — это еще ничего. Для умножения на ноль уже придумали водородные и атомные бомбы типа Fat Boy.
- На испытаниях Су-24 регулярно случался отказ аппаратуры бомбометания. Причем происходило это только в том случае, если на цель заходил летчик-испытатель Ильюшин. Причина оказалось тоже не сложной. Только он заходил на цель с точностью, превышавшей машинную точность. Получался «машинный нуль», после чего шел сбой из-за попытки деления на ноль.
- В интернетах гуляет байка об аналогичном случае: мотороловцы клеили истребитель для Израиля, и он над Мертвым морем (высота над уровнем моря — нулевая или отрицательная) пытался делать сабж и самовыпиливался.
- Алсо, существует одноименный фантастический рассказ за авторством Теда Чана. Текст повествует об учёном-математике, который тронулся умом, внезапно обнаружив полную несостоятельность любимой науки. Мораль проста — гиковство в любой форме до добра не доводит. Такие дела.
- Алсо, у пейссателя есть книжка, где одна зверушка с IQ > 9000 способна буквально войти в кому, пытаясь в уме произвести операцию деления на ноль.
- В эпичной игре «Ядерный Титбит» свою роль в развязке сюжета сыграл суперробот, по всемогуществу сравнимый с Богом. «Когда его включили он начал смеяться. И не перестает до сих пор… Он может вообще все, но его волнует один единственный вопрос: Что будет, если единицу разделить на ноль». Для устранения бага требовались внеземные технологии и человеческий мозг, так как только люди могут держать иррациональность в голове, не сходя с ума.
- Алсо, у этого вашего Алистера Кроули есть
|
Каждое число равно бесконечности: в них нет различия |
- А еще это умеет делать калькулятор андроида (пруфлинк для скачивания) — при делении любого числа на ноль он выдает бесконечность. (При делении ноля на ноль он честно пишет «Ошибка»)
- А в HL2 есть оружие, делящее на ноль всех (в цитадели гравиган меняет цвет и боевые параметры). И AR2 тоже делит, шариком.
- В махо-сейнен манге Mahou Senki Lyrical Nanoha Force у одного из главных героев есть магическое устройство Devider и заклинание Divide by Zero.
- При попытке деления на ноль встроенным калькулятором телефона Sony Ericsson и Nokia всплывает окошко, которое гласит «деление на ноль запрещено». Видимо, сони с нокой решили не мучать себе моск, да и другим тоже. Motorola ZN5 с английским языком при делении на 0 пишет E. Что означает Error — Ошибка — с расово-верного пиндосского языка.
- Встроенный калькулятор Windows 7 знает, что деление на ноль невозможно. Теперь и ты это знаешь. Однако, 0/0 сделать пытается, как всегда, безрезультатно.
- Встроенный калькулятор Mac OS X при делении на ноль, так и пишет: «деление на ноль»
- У братьев Стругацких в «Понедельнике…» делением ноля на ноль (причём с помощью настольных калькуляторов) занимается целый отдел Абсолютного Знания.
- Один из первых процессоров серии Pentium при выполнении операции «деление на ноль» просто напросто зависал; приходилось перезагружать компьютер чудо-кнопкой Reset. Запрос деления на ноль мог возникать в случае коряво написанных программ или же мог быть вызван искуственно посредством Windows-калькулятора. Ошибка была исправлена в следующей модели пня.
- Олимпиады и ногомячные чемпионаты являются вовсе не попыткой создания благоприятной распильной среды, а результатом деления на ноль бюджета этой страны.
- У попсовой группы ВиаГра есть песня «Но я играю эту роль…». Так вот, анонимус однажды IRL слышал, как незнакомая красивая тян исполняла пародию на эту песню, и один из рефренов этой пародии звучал так: «Но я играю эту роль, Делю трёхзначные на ноль, В науке я неутомима. Мне теорема по плечу, Но я бессмертья не хочу, Вези в дурдом меня, любимый!» (Другие рефрены были еще более доставляющими: «…курю табак, пью алкоголь, И мне становится голимо…», «…я из ружья стреляю в моль, Но почему-то чаще мимо…»).
- Формально такими операциями, как деление и умножение на ноль (обычно алиенов, мутантов, роботов и прочей подобной пиздобратии), занимаются герои 95% быдло-фантастических книжонок и YOBA-игр. Пипл хавает и просит добавки.
[править] Помножить на ноль
Малоизвестный, но доставляющий мем. Имеется в виду то, что если число на ноль умножить, то получится ноль (то есть ничего). Пример с этого вашего плейграунда: «Извините, а как можно в Готике воскрешать героев, а то кореш-манчкин всех неписей на ноль помножил?»
[править] Bash.org.ru о делении на ноль
« | |
| Devix: | почему нельзя делить на ноль? Умножать же можно. причем тоже ноль получается. |
| vampir_infernal: | почему нельзя? можно. только результат такого деления — бесконечность |
| Devix: | а почему не ноль? |
| vampir_infernal: | ну вот гляди. 2*0 — это два взять ноль раз, будет ноль. А 2/0 — это «сколько раз ноль умещается в двойке», бесконечность |
| Devix: | если 2/0=х, то значит 2=х*0 и… бля… 2=0. А если 2=0, значит 2/0=0! числитель пропадает в никуда? |
| vampir_infernal: | ну вот чтобы такой х**ней не страдать, математики приняли негласное соглашение, что на ноль делить нельзя |
» | |
—  400734 | |
« | |
| ^_^: | Чего б ты щас хотел? |
| alias: | честно? |
| ^_^: | Честно. |
| alias: | делить на ноль |
» | |
| — 403615 | |
[править] Галерея
| »»» | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
.jpg)
[править] См. также
[править] Ссылки
- Почему же все таки нельзя этого делать. В адаптированном изложении.
 |
[ + ] Деление на ноль — часть точного мира чисел
|
||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|||||||||
 |
[ + ] Капитан заявляет: «Деление на ноль имеет отношение к Башоргу. Так-то!» | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||
